ದೇವರು ಮಕ್ಕಳಿಗೆ ಕ್ಯಾನ್ಸರ್ ಪಡೆಯಲು ಅನುಮತಿಸುತ್ತಾರೆಯೇ? ಇರಬಹುದು...
ಪರೀಕ್ಷಾ ಫೈನಲ್ನಲ್ಲಿ ಗಣಿತದ ಸಮಸ್ಯೆಗೆ ಕರ್ಮ-ಕುನ್ ಅವರ ಉತ್ತರವನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ನಾನು ಪ್ರಯತ್ನಿಸುತ್ತಿದ್ದೇನೆ.
ನಾನು ಉಲ್ಲೇಖಗಳು ಮತ್ತು ಸಮಸ್ಯೆಯ ವಿವರಣೆಯನ್ನು ಹುಡುಕಿದ್ದೇನೆ ಆದರೆ ಯಾವುದೇ ಪ್ರಯೋಜನವಾಗಿಲ್ಲ. ಸಮಸ್ಯೆಯ ಭಯಾನಕ ವಿವರಣೆಗಳನ್ನು ನನಗೆ ಇನ್ನೂ ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ಸಾಧ್ಯವಾಗಲಿಲ್ಲ, ಮತ್ತು ಅವರ ಆಲೋಚನಾ ಪ್ರಕ್ರಿಯೆಯು ನಿಮಗೆ ತಿಳಿದಿದೆ ಎಂದು ಉತ್ತರವು umes ಹಿಸುತ್ತದೆ, ಅದು ನನಗೆ ತಿಳಿದಿಲ್ಲ.
ಇದು ಸಮಸ್ಯೆಯ ಇಂಗ್ಲಿಷ್ ಅನುವಾದವನ್ನು ಹೊಂದಿದೆ:
young-il-long-kiyoshi.tumblr.com/post/125623681248/on-the-topic-of-the-final-maths-question-in-the
ಮತ್ತೊಂದು ಲಿಂಕ್ ನಾನು ಸಮಸ್ಯೆಯನ್ನು ಪ್ರಸ್ತಾಪಿಸುತ್ತಿದ್ದೇನೆ ಆದರೆ ಅದನ್ನು ವಿವರಿಸುತ್ತಿಲ್ಲ.
angryanimebitches.com/2016/03/assassination-classroom-season-2-episode-12-the-principal-is-a-sore-loser/
ಅವುಗಳು ಯೂಟ್ಯೂಬ್ ವಿಡಿಯೋ ಆಗಿದ್ದು ಅದು ಕರ್ಮ-ಕುನ್ ಅವರ ಉತ್ತರವನ್ನು ವಿವರಿಸುತ್ತದೆ ಆದರೆ ಅವರ ವಿವರಣೆಯೂ ಸಹ ಕೇಂದ್ರ ಪರಮಾಣುವಿನ ವಿಸ್ತೀರ್ಣವು ಘನದ ಅರ್ಧದಷ್ಟು ಪ್ರದೇಶವನ್ನು ಎರಡು ಭಾಗಿಸಿದಾಗ ಸಮನಾಗಿರುತ್ತದೆ ಎಂಬ ತೀರ್ಮಾನಕ್ಕೆ ಅವನು ಹೇಗೆ ಬಂದಿದ್ದಾನೆಂದು ನನಗೆ ಇನ್ನೂ ಅರ್ಥವಾಗುತ್ತಿಲ್ಲ. a ^ 3/2
ವೀಡಿಯೊ ಲಿಂಕ್: ವಿಲಕ್ಷಣ ಜ್ಯಾಮಿತಿ (ಹತ್ಯೆ ತರಗತಿ ಎಸ್ 2 ಇ 12)
ನಾನು ಇದನ್ನು ಪೋಸ್ಟ್ ಮಾಡಲು ಕಾರಣವೆಂದರೆ, ಥ್ರೆಡ್ನಲ್ಲಿ ಕೇಳದೆ ಸಮಸ್ಯೆಯನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ನನಗೆ ಬೇರೆ ದಾರಿ ಇಲ್ಲ.
"ಹೈಸ್ಕೂಲ್" ದೃಷ್ಟಿಕೋನದಲ್ಲಿ ಉತ್ತರದ ವಿವರಣೆಯನ್ನು ನಾನು ಬಯಸುತ್ತೇನೆ, ವೃತ್ತಿಪರ ಪಿಎಚ್ಡಿ ಮಟ್ಟವಲ್ಲ ...
"ಈಕ್ವಿಡಿಸ್ಟೆಂಟ್", "ಇನ್ಫಿನಿಟೈಸಿಮಲ್", "ಶೃಂಗ" ಅಥವಾ ನಾನು ಗ್ರಹಿಸಲಾಗದ ಯಾವುದೇ ತಾಂತ್ರಿಕ ಪದಗಳನ್ನು ಕೇಳಲು ನಾನು ಬಯಸುವುದಿಲ್ಲ.
ನಾನು ತುಂಬಾ ಬೇಡಿಕೆಯಿದ್ದೇನೆ ಎಂದು ನನಗೆ ತಿಳಿದಿದೆ, ಆದರೆ ದಯವಿಟ್ಟು ಕರ್ಮ-ಕುನ್ ಹೇಗೆ ಸಿಕ್ಕಿತು ಎಂಬುದನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ನನಗೆ ಸಹಾಯ ಮಾಡಿ a ^ 3/2. ನಾನು ಕರ್ಮದಿಂದ ಪಡೆದ ಏಕೈಕ ದೃಷ್ಟಿಕೋನವೆಂದರೆ ಎಲ್ಲಾ 8 ಪರಮಾಣುಗಳು ತಮ್ಮದೇ ಆದ ಘನವನ್ನು ರೂಪಿಸುತ್ತವೆ, ಮತ್ತು ಆ ಕಾಲ್ಪನಿಕ ಘನದ ಮಧ್ಯದ ಬಿಂದುವು 8 ಪ್ರತ್ಯೇಕ ಘನಗಳೊಳಗಿನ ಎಲ್ಲಾ ಪರಮಾಣುಗಳಿಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
ಮತ್ತು ವೀಡಿಯೊವು ಹಾಗೆಯೇ ಹೇಳುತ್ತದೆ, ಆದರೆ ಜಗತ್ತಿನಲ್ಲಿ ಅದು ಹೇಗೆ ಹೋಗಿದೆ ಎ 1/8 ಗೆ 2 ಎ? ತದನಂತರ a ^ 3/2
ಇಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ:
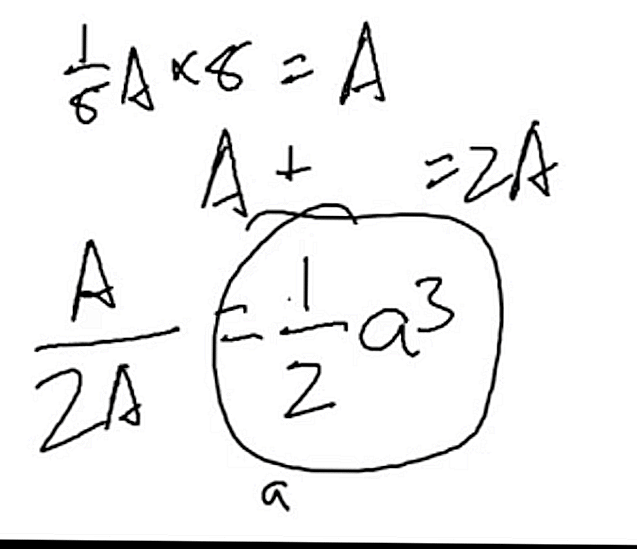
- ಅಸಾನೊ-ಕುನ್ ಅವರ ಪರಿಹಾರ ವಿಧಾನಕ್ಕಾಗಿ, ನಾನು ಭಾವಿಸುತ್ತೇನೆ? math.stackexchange.com/questions/3193480/…
ಸ್ಫಟಿಕ ಲ್ಯಾಟಿಸ್ನಲ್ಲಿನ ಎಲ್ಲಾ ಪರಮಾಣುಗಳು ಒಂದೇ ಆಗಿರುತ್ತವೆ. ಶೃಂಗದಲ್ಲಿರುವ ಪರಮಾಣುವಿನ ಪರಿಮಾಣವನ್ನು ಹೇಳೋಣ (ಮೂಲೆಯಲ್ಲ, ಅದು ಒಂದು ಮೂಲೆಯಾಗಿದ್ದರೆ, ನಿಮಗೆ ಸ್ವಲ್ಪ ವಿಭಿನ್ನವಾದ ತಾರ್ಕಿಕತೆಯ ಅಗತ್ಯವಿರುತ್ತದೆ) ಬಿ. ಶೃಂಗದ ಪ್ರತಿಯೊಂದು ಪರಮಾಣು ಘನದ (1/8) ಬಿ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ. ರೇಖಾಚಿತ್ರವನ್ನು ನೋಡಿ.
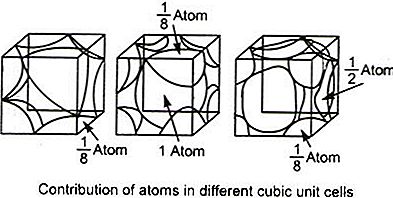
ಉದ್ದ a ಹೊಂದಿರುವ ಘನಕ್ಕಾಗಿ, ಇದು ಘನ ಪರಮಾಣು A ಯನ್ನು ಪರಿಮಾಣ D ಯೊಂದಿಗೆ ಮತ್ತು 8 ಪರಮಾಣುಗಳನ್ನು ಶೃಂಗಗಳಲ್ಲಿ ಹೊಂದಿರುತ್ತದೆ, ಪ್ರತಿಯೊಂದೂ ಘನದ (1/8) B ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ. ಹೀಗಾಗಿ,
ಎ3 = ಡಿ + 8 × (1/8) ಬಿ
ಆದಾಗ್ಯೂ, ಶೃಂಗಗಳಲ್ಲಿನ ಪರಮಾಣುಗಳು ವಾಸ್ತವವಾಗಿ ಕೇಂದ್ರ ಪರಮಾಣುವಿಗೆ ಹೋಲುತ್ತವೆ ಎಂದು ನಮಗೆ ತಿಳಿದಿರುವ ಕಾರಣ, ಬಿ ಪರಿಮಾಣವು ಡಿ ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಮತ್ತು ಆದ್ದರಿಂದ,
ಎ3 = ಬಿ + 8 × (1/8) ಬಿ ==> ಬಿ = (1/2) ಎ3
ಕ್ಯೂಇಡಿ
ನೀವು ಪ್ರಸ್ತಾಪಿಸಿದ ಎಲ್ಲಾ ತಾಂತ್ರಿಕ ಪದಗಳು ನನ್ನ ಪ್ರೌ school ಶಾಲೆಯಲ್ಲಿ ನಾನು ಕಲಿಯುತ್ತಿದ್ದೆ. ಕರ್ಮ ಹೇಳಿದಂತೆ ಈ ಪ್ರಶ್ನೆ ಕಠಿಣವಲ್ಲ. ಇದು ಗಣಿತ ಮತ್ತು ರಸಾಯನಶಾಸ್ತ್ರದ ಸಂಯೋಜಿತ ಪ್ರಶ್ನೆಯಾಗಿದೆ.
7- 1 ಆದರೆ ನೀವು ಇದನ್ನು ಗಣಿತ ವೇದಿಕೆಯಲ್ಲಿ ಕೇಳಬೇಕು ಮತ್ತು ಇಲ್ಲಿ ಅಲ್ಲ ಎಂದು ನಾನು ಭಾವಿಸುತ್ತೇನೆ. ಇದು ವಿಚಿತ್ರವಾಗಿ ಕಾಣುತ್ತದೆ.
- ಆದರೆ ಅದು ಏಕೆ 2 ಕ್ಕಿಂತ ಹೆಚ್ಚು ಸೂತ್ರದಲ್ಲಿ ^ 3/2 ??
- 2 ಕ್ಕಿಂತ ಹೆಚ್ಚು ಇಲ್ಲಿ ನಿಮಗೆ ಹೇಳುತ್ತದೆ, ಒಂದು ಘನಕ್ಕೆ, ಪರಿಮಾಣದ ಅರ್ಧದಷ್ಟು ಮಾತ್ರ ನಿರ್ದಿಷ್ಟ ಪರಮಾಣು ಎ ತೆಗೆದುಕೊಳ್ಳುವ ಪರಿಮಾಣವಾಗಿರುತ್ತದೆ, ಉಳಿದ ಪರಿಮಾಣವನ್ನು ಇತರ ಪರಮಾಣುಗಳು ಹಂಚಿಕೊಳ್ಳಬೇಕು.
- ಹಾಗಾಗಿ ನಾನು ನಿಮ್ಮನ್ನು ಸರಿಯಾಗಿ ಅನುಸರಿಸುತ್ತಿದ್ದರೆ, ಎ / 8 * 8 = ಎ, ಮತ್ತು ಎಂಟು ಶೃಂಗಗಳು 2 ಪರಮಾಣುಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತವೆ, ಅಂದರೆ 2 ಎ. ನಂತರ ಎ ಘನದ ಅರ್ಧ, ನಂತರ ನಾವು ಮಾಡುತ್ತೇವೆ ಎ / 2 ಎ... ಮತ್ತು ಪರಮಾಣುವಿನ ಪರಿಮಾಣವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ನಾವು ಗುಣಿಸುತ್ತೇವೆ x, y, z ಅದು 3D ಮತ್ತು ಘನದ ಪ್ರದೇಶವನ್ನು ಕಂಡುಹಿಡಿಯಲು ನಾವು ಸೂತ್ರದೊಂದಿಗೆ ಕೊನೆಗೊಳ್ಳುತ್ತೇವೆ a ^ 3 ಸರಿ? ನಂತರ ನಾವು ಅದನ್ನು ಅರ್ಧದಷ್ಟು ಮಾಡುತ್ತೇವೆ 2 ಕ್ಕಿಂತ ಹೆಚ್ಚು? a ^ 3/2
- ಇಲ್ಲ, ಶೃಂಗದಲ್ಲಿರುವ ಎಂಟು ಪರಮಾಣುಗಳು ಘನದಲ್ಲಿ ಒಂದು ಪರಮಾಣುವಿನ ಜಾಗವನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತವೆ. ಕೇಂದ್ರ ಪರಮಾಣು ಮತ್ತು ಶೃಂಗಗಳಲ್ಲಿನ ಪರಮಾಣುಗಳನ್ನು ಒಳಗೊಂಡಿರುವ ಒಟ್ಟು ಪರಿಮಾಣಕ್ಕೆ ಕೇಂದ್ರ ಪರಮಾಣು ತೆಗೆದುಕೊಂಡ ಪರಿಮಾಣದ ಅನುಪಾತವನ್ನು ಕಂಡುಹಿಡಿಯಲು ಎ / 2 ಎ ಅನ್ನು ಬಳಸಲಾಗುತ್ತದೆ. ಆದ್ದರಿಂದ, ಪರಮಾಣು ಎ ಘನದ ಪರಿಮಾಣದ 1/2 ಅನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ ಮತ್ತು ಆದ್ದರಿಂದ ^ 3/2 ಎಂದು ನಮಗೆ ತಿಳಿದಿದೆ.
ನಾನು ಈ ಪ್ರಶ್ನೆಗೆ ತಡವಾಗಿ ಬಂದಿದ್ದೇನೆ ಎಂದು ನನಗೆ ತಿಳಿದಿದೆ, ಆದರೆ ಇಲ್ಲಿ ಬಹುಶಃ ಸರಳವಾದ ವಿವರಣೆಯಿದೆ. ನಾನು ಅನಿಮೆನಲ್ಲಿ ಈ ಸಮಸ್ಯೆಯನ್ನು ಎದುರಿಸಿದ್ದೇನೆ ಮತ್ತು ಅವರು ಉತ್ತರವನ್ನು ಬಹಿರಂಗಪಡಿಸುವ ಮೊದಲು ಅದನ್ನು ಪರಿಹರಿಸಲು ಬಯಸುತ್ತೇನೆ.
ಸರಿ. ನೀವು ಮಧ್ಯದಲ್ಲಿ ಪರಮಾಣುವಿನೊಂದಿಗೆ ಘನವನ್ನು ಹೊಂದಿದ್ದೀರಿ. ನೀವು ಮಾಡಲು ಬಯಸುವುದು ಘನವನ್ನು ಎಂಟು ತುಂಡುಗಳಾಗಿ ಒಡೆಯುವುದು. ಈ ತುಂಡುಗಳಲ್ಲಿ ಒಂದನ್ನು ತೆಗೆದುಕೊಳ್ಳಿ. ವಿರುದ್ಧ ಮೂಲೆಗಳಲ್ಲಿ ಎರಡು ಪರಮಾಣುಗಳಿವೆ (ಶೃಂಗಗಳು). ಈ ಪರಮಾಣುಗಳಲ್ಲಿ ಒಂದು ಕೇಂದ್ರ ಪರಮಾಣು [ಎ] 0 ಮತ್ತು ಇನ್ನೊಂದು ಅಂಚಿನಲ್ಲಿರುವ ಪರಮಾಣು. ಒಂದು ಸರಳ ತರ್ಕದ ಪ್ರಕಾರ ಈ ಘನದ ಎಂಟನೆಯ ಅರ್ಧದಷ್ಟು ಭಾಗವು ಒಂದು ಪರಮಾಣುವಿಗೆ ಇನ್ನೊಂದಕ್ಕಿಂತ ಹತ್ತಿರದಲ್ಲಿದೆ. ಇದು ಇತರ ಎಲ್ಲ 8 ತುಣುಕುಗಳಿಗೆ ಹೋಗುತ್ತದೆ, ಆದ್ದರಿಂದ ಕೇಂದ್ರದ ಪರಮಾಣುವಿಗೆ ಹತ್ತಿರವಿರುವ ಘನದ ಪರಿಮಾಣವು ಒಟ್ಟು ಪರಿಮಾಣದ ಅರ್ಧದಷ್ಟಿರುತ್ತದೆ.
ಸಮಸ್ಯೆ ಗೋಚರಿಸುವುದಕ್ಕಿಂತ ಹೆಚ್ಚು ಸರಳವಾಗಿದೆ ಮತ್ತು ನಾನು ಮೂಕನಾಗಿರುವುದನ್ನು ಅರಿತುಕೊಳ್ಳುವ ಮೊದಲು ಪರಿಮಾಣವನ್ನು ಜ್ಯಾಮಿತೀಯ ತುಣುಕುಗಳ ಮೂಲಕ ಲೆಕ್ಕಾಚಾರ ಮಾಡುವುದನ್ನು ಒಪ್ಪಿಕೊಳ್ಳುತ್ತೇನೆ. ಇದಕ್ಕೆ ಹೆಚ್ಚು ಗಣಿತ ಅಗತ್ಯವಿಲ್ಲ. ಕೇವಲ ತರ್ಕದ ದೃ gra ವಾದ ಗ್ರಹಿಕೆ ಮತ್ತು ಸ್ವಲ್ಪ ಬುದ್ಧಿವಂತಿಕೆ.
ಬಹುಶಃ, ಮಂಗಾದಲ್ಲಿನ ಉತ್ತರವು ಸಹ ಸರಿಯಾಗಿಲ್ಲ. ಪರಮಾಣುಗಳು ಪ್ರತಿ ಘನದೊಳಗೆ ಒಂದೇ ಪ್ರಮಾಣದ ಜಾಗವನ್ನು ಆಕ್ರಮಿಸಿಕೊಂಡರೆ, ಅವು (ಎ) - ಅಗೋಚರ ರೇಖೆಗಳು) ಅರ್ಧದಷ್ಟು ಇರುತ್ತದೆ. ಗೋಳದ ಪರಿಮಾಣವನ್ನು ಪರಿಹರಿಸುವ ಸೂತ್ರಕ್ಕೆ ನೀವು ಅದನ್ನು ಮೂಲಭೂತವಾಗಿ ಪ್ಲಗ್ ಮಾಡಬಹುದು, ಅದು ನಾಲ್ಕು ಪಟ್ಟು ಮೂರು ಪಟ್ಟು ಪೈ ಬಾರಿ ಆರ್ 3 ಅನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ನಿಮ್ಮ ಆರ್ (ತ್ರಿಜ್ಯ) ಒಂದು / 2 (ಏಕೆಂದರೆ ಪರಮಾಣುಗಳು ಒಂದೇ ಆಗಿರುತ್ತವೆ ಜಾಗದ ಪ್ರಮಾಣ, ಆದ್ದರಿಂದ ಒಂದು ಪರಮಾಣು ಅದೃಶ್ಯ ರೇಖೆಯ ಅರ್ಧದಷ್ಟು ಭಾಗವನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ)
ಮೂಲತಃ, ನೀವು ವಿ = 4/3 * π * (ಎ / 2) ^ 3 ಮಾಡುತ್ತೀರಿ
ವಿ = 4/3 * * ಎ ^ 3/8
ವಿ = 4 (4/3 ರಲ್ಲಿ) 8 ಅನ್ನು ರದ್ದುಗೊಳಿಸುತ್ತದೆ (^ 3/8 ರಲ್ಲಿ) ಆದ್ದರಿಂದ ನೀವು 1/3 * π * a ^ 3/2 ಅನ್ನು ಪಡೆಯುತ್ತೀರಿ
ವಿ = π * ಎ ^ 3/6
ಇತರೆ: * = ಬಾರಿ, ^ = ಶಕ್ತಿಗೆ, π = pi.



